Harry Markowitz a jeho model| Teorie portfolia a efektivní hranice.

Markowitz model a jeho efektivní hranice jsou pojmy, které jsme někdy slyšeli během studia na ekonomických fakultách. Nicméně, po letech nevíme přesně, jaké jsou jejich hlavní postuláty a jak nám mohou pomoci diverzifikovat naše riziko při výběru aktiv, která zařazujeme do našeho portfolia.

Hloubka teorie výběru portfolia a následné evoluce se nevejdou do jednoho článku, ale tento má za cíl být základním shrnutím pro pochopení a použití tohoto nástroje prostřednictvím klíčových otázek.

Ale pojďme postupně, než vysvětlíme, co to je a jak se vyvíjí, přejděme k jednodušším definicím.

Co je efektivní portfolio?

Efektivní portfolio je takové, které splňuje dvě podmínky:

• Pro svou očekávanou úroveň výnosu neexistuje žádné jiné portfolio, které by mělo nižší riziko.
• Pro riziko, které nese, neexistuje jiná investiční příležitost, která by umožnila dosáhnout vyššího očekávaného výnosu, tedy poskytuje maximální možný očekávaný výnos pro svou úroveň rizika.

Tímto způsobem, abyste toho dosáhli, zde jsou některé rady, které byste jako investor mohli následovat:

1. Poznejte svůj investiční profil: To znamená, jaké riziko jste jako investor ochotni přijmout: konzervativní, střední nebo agresivní.

2. Definujte realistické cíle: Je třeba vědět, jaký je cíl, nebo jinými slovy, jaký výnos chci dosáhnout, s vědomím úrovně rizika, kterou chci přijmout. Proto je třeba klást důraz na výraz "realistické cíle", protože:

• Přehnané cíle by mohly vést k demotivaci.
• Méně ambiciózní cíle by mohly vést k uvolnění a dlouhodobě k ztrátám z důvodu nadměrné důvěry.

3. Vyvážení rizika: Nyní, když známe naši úroveň rizika a cíle, které chceme dosáhnout, je čas rozdělit riziko mezi různé aktiva jako akcie, ETF, CFD, fondy...

4. Poradenství v oblasti daní: Po promyšlení plánu, strategie a především po podstoupení veškerého rizika, kterému jsme byli vystaveni, přichází nejtraumatičtější okamžik ze všech, projít pokladnou. Daně. K tomu je zásadní být informován o tom, jak podat daňové přiznání, aby zahrnovalo výnosy z kapitálu, nebo přímo vyhledat odborníka, jinak by nám jakákoli pokuta od finančního úřadu mohla způsobit ztrátu toho, co nás stálo tolik práce a rizika získat.

5. Diverzifikujte své portfolio na základě rizika: Doposud jsme nepřestali mluvit o investování na burze, ale ve skutečnosti existuje mnoho dalších výnosných a možná méně rizikových forem investic: Pasivní příjmy, nemovitosti...

1. Co je Markowitz model?

A nyní, když už víme, jak by mělo být nastaveno efektivní portfolio, je čas začít hodnotit Markowitzův model. Zatímco Harry Markowitz vytvořil základní teorie diverzifikace, Bogle je převedl do dostupné investiční praxe

Markowitz model je matematický model používaný k analýze výkonnosti investičních portfolií a byl vyvinut ekonomem Harrym Markowitzem během 50. let 20. století.

Tímto způsobem Markowitz slouží k maximalizaci výnosu minimalizací rizika, k tomu vytváří diverzifikované portfolio v několika třídách aktiv. Tato diverzifikace pomáhá snižovat celkové riziko a zároveň umožňuje dosáhnout vysokého potenciálního výnosu.

V současné době má tento model obrovský vliv v oblasti financí a stále je používán investory a správci peněz po celém světě.

Kdo je Harry Markowitz?

Ekonom Henry Markowitz se narodil v roce 1927 v Chicagu, Illinois.

Patřící k prestižní Chicagské ekonomické škole se stal jedním z nejvýznamnějších investičních analytiků na světě a v roce 1952 napsal článek „Portfolio Selection“ založený na své disertační práci, který ovlivnil jeho kariéru a otevřel nové pole ve studiu optimálního složení portfolia cenných papírů.

V roce 1990 obdržel Nobelovu cenu za ekonomii spolu s Millerem a Sharpem za příspěvky k teorii správy portfolia.

Jaké jsou předpoklady, na kterých je založen Markowitzův model?

Předpoklady o chování a racionální metodě volby investora

• Všichni jednotlivci se chovají racionálně a proto maximalizují svou očekávanou užitkovou funkci.
• Očekávaná užitková funkce investora závisí pouze na očekávaném výnosu jako měřítku ziskovosti a na varianci nebo směrodatné odchylce jako měřítku rizika.
• Užitkové funkce investorů jsou monotónně rostoucí, takže pro portfolio s toutéž variancí se preferuje portfolio s vyšším očekávaným výnosem.
• Investoři mají averzi k riziku, takže pro portfolio s týmž očekávaným výnosem se preferuje portfolio s nižší variancí.
• Indiferenční nebo izoužitkové křivky jsou rostoucí (čím vyšší riziko, tím vyšší požadovaný výnos) a konvexní (čím vyšší riziko, tím více se zvyšuje požadovaný výnos) a ukazují kombinace výnos-riziko, které poskytují stejnou užitkovost investorovi. Křivky umístěné více vlevo a nahoru představují vyšší úrovně očekávané užitkovosti.

Předpoklady o aktivech a finančních trzích

1. Předpokládá se, že finanční trhy jsou dokonalé:

• Všechny informace jsou stejně dostupné a zdarma pro všechny účastníky trhů.
• Neexistují transakční náklady při nákupu a prodeji finančních aktiv.
• Cenné papíry jsou nekonečně dělitelné. Je možné do nich investovat jakoukoli část rozpočtu.
• V ekonomice není inflace ani daně.
• Investoři jsou cenově akceptující.

2. Všichni investoři mají stejnou šíři svého plánovacího horizontu, který je jedno období. Na začátku období získají určité portfolio, které prodají na konci daného období.

3. Na finančních trzích se obchoduje s N rizikovými finančními aktivy a jejich kombinacemi. Nezvažuje se existence bezrizikového finančního aktiva, do kterého by bylo možné investovat nebo s nímž by bylo možné financovat.
4. Hodnoty mají okamžitou likviditu na konci referenčního období.
5. Nejsou povoleny prodeje na krátko.

Jak se vyvíjí Markowitzův model?

Model navržený Markowitzem má za cíl určit optimální portfolio, tedy takové, které maximalizuje očekávaný užitek investora.
K tomu určuje čtyřstupňový proces, který spočívá v:

1. Určení souboru investičních možností, které trh nabízí (životaschopný soubor)

• Analyzují se N riziková aktiva a možné portfolia, která se obchodují na trzích, odhaduje se jejich očekávaná výnosnost, variance a kovariance mezi výnosy každého páru možných finančních aktiv.
• S dvěma tituly se střední korelací se kombinace nacházejí na hyperbole nakreslené mezi takovými hranicemi, přičemž stupeň zakřivení je větší, čím menší je korelace mezi výnosy dvou aktiv.
• S N finančními aktivy a střední korelací je to oblast, kterou nazýváme životaschopný soubor.

2. Určení efektivní hranice.

Připomeňme si, že efektivní portfolio je takové, které splňuje dvě podmínky.

• Pro svou úroveň očekávaného výnosu neexistuje žádné jiné portfolio, které by mělo nižší riziko.
• Pro riziko, které s sebou nese, neexistuje jiná investiční příležitost, která by umožnila dosáhnout vyššího očekávaného výnosu, tedy poskytuje maximální možný očekávaný výnos pro svou úroveň rizika.

Tedy efektivní hranice je koncept Markowitzova modelu, který naznačuje, že existuje optimální rovnováha mezi rizikem a výnosem při investování. Tato rovnováha se dosahuje diverzifikací investic do různých tříd aktiv a obvykle se znázorňuje ve formě grafu, s výnosem na ose x a rizikem na ose y. Křivka efektivní hranice představuje optimální portfolio pro danou úroveň rizika.

Například investor s averzí k riziku by si vybral portfolio blíže k ose Y (Ep, nízké riziko), zatímco investor hledající vysokou návratnost by si vybral portfolio blíže k ose X (vysoká návratnost). Tímto způsobem efektivní hranice jsou různé optimální body mezi návratností a rizikem a určí nám, v závislosti na riziku, které jsme ochotni podstoupit, jakou návratnost bychom měli požadovat a naopak.

V jakémkoli jiném případě se považuje portfolio za neefektivní. Efektivní portfolio s nejnižším rizikem je portfolio minimální variance (CMV) a efektivní hranice začíná u CMV.

3. Specifikace preferencí investora

• Křivky lhostejnosti jsou rostoucí a konvexní. Konkrétní tvar bude záviset na stupni averze k riziku investora.
• Křivka lhostejnosti nebo izo-užitková křivka je grafické znázornění všech kombinací očekávaného výnosu a rizika, které poskytují investorovi stejnou očekávanou užitkovost a jsou mu lhostejné.

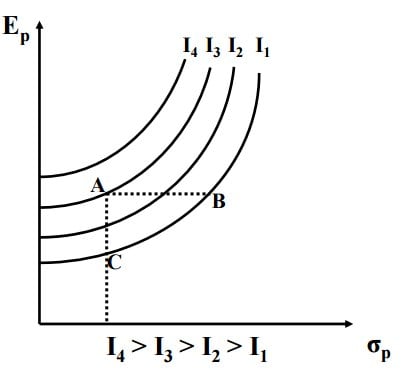
4. Určení optimálního portfolia

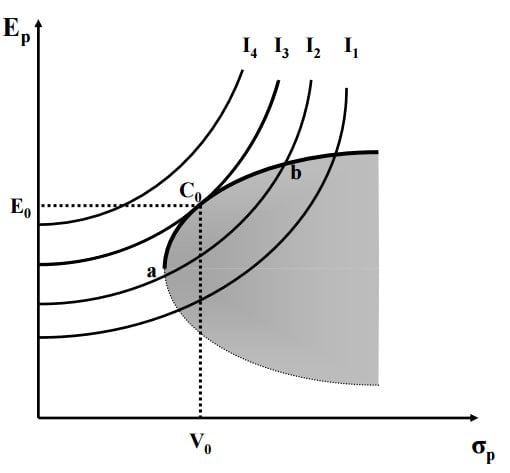
• Optimální portfolio se nachází v bodě dotyku mezi efektivní hranicí a izo-užitkovou křivkou. Portfolio O je to, které poskytuje nejvyšší možnou užitkovost tím, že se nachází na nejvyšší křivce lhostejnosti.
• Je jedinečné pro každého investora, protože závisí na:
  • Individuálních odhadech o cenných papírech (efektivní hranice)
  • Stupni averze k riziku (křivky lhostejnosti)

4- Jak se model analyticky rozvíjí?

Sada efektivních portfolií může být vypočítána řešením následujícího parametrického kvadratického programu:

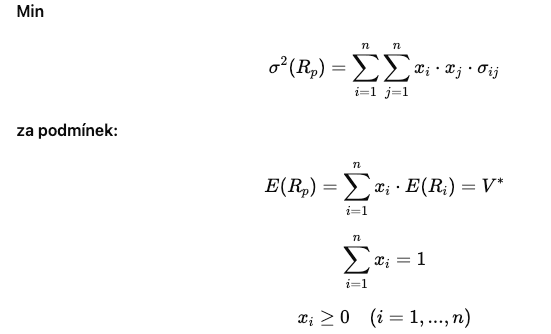
• Xi: je podíl rozpočtu investora určený pro finanční aktivum
• i: neznámá proměnná programu
• σ^2 (Rp): rozptyl portfolia p
• ij: Kovariance mezi výnosy cenných papírů i a j
• E(Rp): očekávaná návratnost nebo výnosnost portfolia p

Množina dvojic [E(Rp), σ^2 (Rp)] nebo kombinace návratnost-riziko všech efektivních portfolií se nazývá «efektivní hranice». Jakmile je tato hranice známa, investor si podle svých preferencí vybere své optimální portfolio.

Vědeli jste, že Ray Dalio, podobně jako Markowitz, staví své portfoliové strategie na hluboké diverzifikaci rizika.

5- Jaké nevýhody má Markowitzův model?

• Matematická složitost modelu: původně bylo navrženo, že řešení algoritmu je složité a že vysoký počet odhadů očekávaných výnosů, rozptylů a kovariancí k výpočtu byl velmi vysoký. Je však třeba zdůraznit, že dnes se s vhodným hardwarem a softwarem řešení značně zjednodušuje.
• Hypotézy modelu: Markowitzův model nebere v úvahu transakční náklady ani daně a navíc předpokládá dokonalou dělitelnost vybraných cenných papírů. Tyto nevýhody lze vyřešit zavedením nových omezení do modelu.
• Hodnocení rizika: model neposkytuje žádný nástroj, který by investorovi umožnil zhodnotit jeho postoj k riziku a odvodit jeho užitkovou funkci, což je nezbytné pro určení jeho optimálního portfolia.
• Použitá data: Michaud (1989) považuje použití historických výnosových řad při odhadu očekávaných parametrů za zdroj významných zkreslení. Proto se efektivní portfolia v modelu skládají z aktiv s vysokou návratností, nízkým rozptylem a nízkou korelací s jinými aktivy, což vede k portfoliím vysoce koncentrovaným do několika titulů (nízká diverzifikace a vysoké riziko). Tuto obtíž však lze vyřešit zavedením dodatečných omezení, která omezí maximální procento zdrojů, které budou investovány do každého titulu.

Markowitzův model je považován za výchozí bod moderní teorie výběru portfolia a určení efektivní hranice. Jeho přístup a následné příspěvky a vývoje jsou bezpochyby jedním z velkých pokroků ekonomické teorie ve 20. století. Nicméně jeho praktické využití investičními manažery a analytiky bylo relativně omezené ve srovnání s jeho teoretickým významem.

Markowitz ve svých studiích dokazuje, že klíčem k diverzifikaci portfolia není jednoduše počet akcií, které ho tvoří, ale korelace jejich výnosů. Pokud je korelace vysoká, nebude možné diverzifikovat, naopak pokud je korelace nízká, bude možné diverzifikovat a riziko bude mnohem menší.