Indikátory
Efektivní využití klouzavého průměru
Klouzavý průměr (Moving Average) je často používaným nástrojem mezi mnoha obchodníky a investory. Umožňuje rozpoznat současné trendy, potenciální obraty v cenovém grafu a také správné okamžiky pro vstup nebo výstup z pozice.
Indikátory Moving Average patří mezi nejzákladnější a nejčastěji využívané nástroje v technické analýze trhu. Slouží jako statistický ukazatel pro vyhlazení cenových dat a identifikaci trendů na finančních trzích. Jejich princip spočívá ve výpočtu průměru ceny nebo jiného ukazatele za určité časové období, přičemž se tento průměr postupně posouvá s každým novým obchodním dnem nebo časovým intervalem. V burzovní analýze se nejčastěji používají 3 klouzavé průměry: jednoduchý, exponenciální nebo EMA a vážený (Rozdíl mezi nimi vysvětlíme později na příkladu).
Klouzavé průměry
Klouzavé průměry se používají k detekci trendů, podpor a odporů. Také nám poskytují signály pro vstup a výstup, a to se stane když cena protne klouzavý průměr. Tento ukazatel se často používá v technické analýze.
Obvykle se kombinují klouzavé průměry různých časových období:
- Krátkodobé: mezi 3 a 25 obdobími
- Střednědobé: mezi 30 a 75 obdobími
- Dlouhodobé: mezi 100 a 250 obdobími
Mezi nejdůležitější průměry patří 50 a 200 denní indikátor, který slouží jako reference pro většinu investorů.
Ve výchozím nastavení se klouzavé průměry počítají na základě závěrečné ceny, i když některé strategie mohou být také založeny na výpočtu klouzavých průměrů na základě otevírací ceny, maximální nebo minimální ceny vybraného období (den, hodina, minuta...).
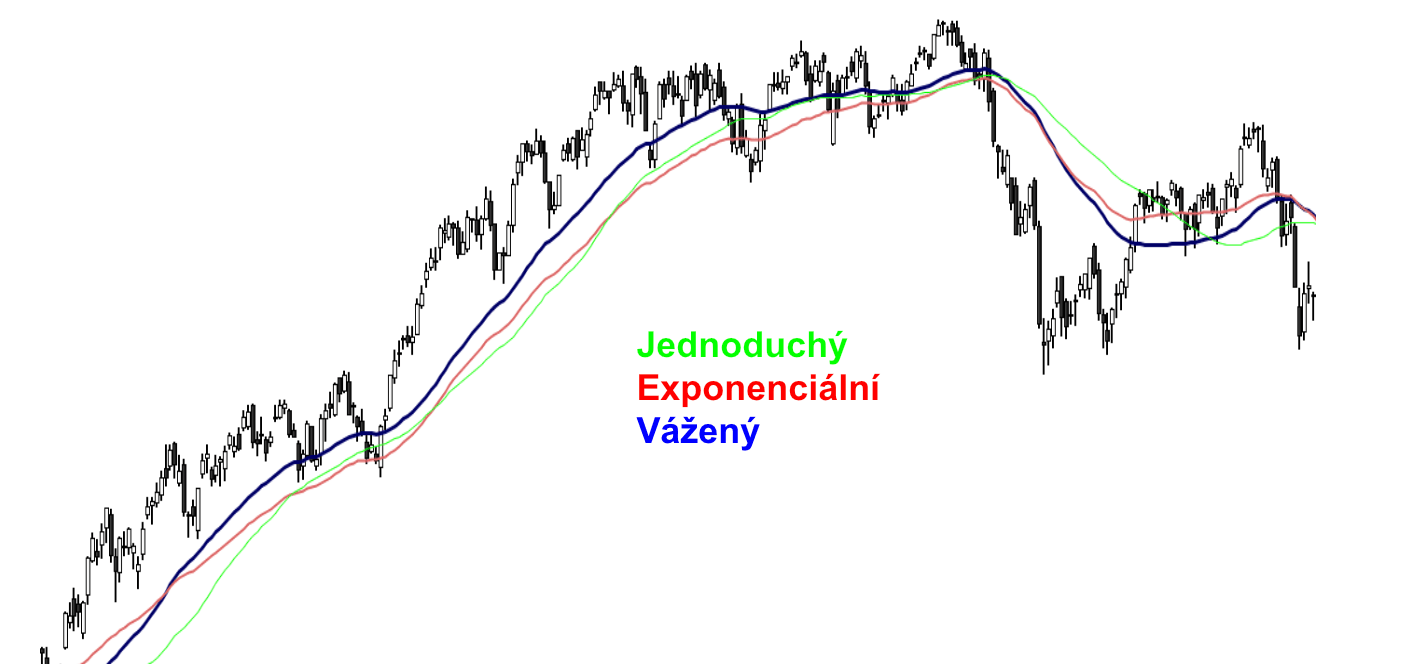
Na grafu vidíme srovnání klouzavého průměru za 50 období, ale se 3 různými přístupy. Vážený průměr je ten, který se nejvíce přibližuje vývoji ceny, zatímco jednoduchý je ten, který se nejvíce vzdaluje když cena kolísá.
Jednoduchý klouzavý průměr
Tento ukazatel sčítá cenu za určený počet období a dělí ji počtem zvolených období, takže vypočítává průměr.
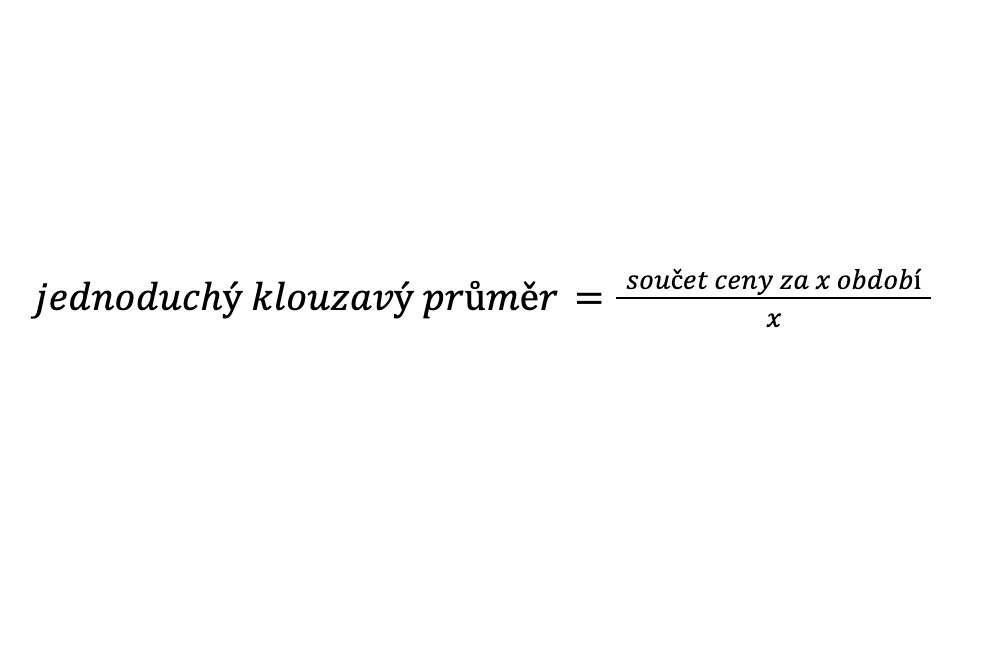
Jednoduchý průměr za 20 dní sčítá cenu (závěrečnou) aktiva za posledních 20 dní a výsledek dělí 20. Tato operace se aktualizuje s novými příchozími daty, přičemž se stará data vyřazují, takže vždy získáme jednoduchý klouzavý průměr za posledních 20 seancí.
Exponenciální klouzavý průměr
Exponenciální průměr se snaží dát větší důraz na nejnovější kotace pomocí vážení nebo exponenciálního vyhlazení. Vyhlazovací faktor je 2/(Období+1). Tímto způsobem se podaří vyhladit cenovou řadu, což umožňuje jasněji detekovat trend aktiva.
Při větším vážení posledních cen, je citlivější na změny trendu, předbíhá jednoduchý a vážený klouzavý průměr.
Vážený klouzavý průměr
Vážený klouzavý průměr se snaží přiřadit progresivní důležitost novějším cenám ve srovnání se staršími cenami, které se počítají. Cílem je vyhladit cenovou řadu, stejně jako exponenciální klouzavý průměr, ale s různými váhami.
Tento průměr se vypočítává tak, že se přiřadí série vah, které se snižují s tím, jak je cena starší, takže nejnovější cena má největší váhu a nejstarší cena nejmenší váhu.
Tímto způsobem se dosáhne podobného efektu jako u exponenciálního klouzavého průměru, protože umožňuje jasněji pozorovat směr jeho trendu.
Strategie s klouzavými průměry
Následující strategie jsou postavené na klouzavých průměrech:
- Lze vypočítat klouzavé průměry různých období, aby se zjistilo, zda se kříží mezi sebou. Například, pokud mám krátkodobý průměr 25 dní a kříží se zdola nahoru s dlouhodobým klouzavým průměrem (např. 100 dní), jedná se o nákupní signál. Pokud by směr křížení byl opačný, tj. shora dolů nebo sestupný, signál by byl prodejní.
- Lze také navrhnout strategie s grafem ceny a grafem jejího klouzavého průměru. Pokud cena překročí klouzavý průměr směrem nahoru, je to nákupní signál. Naopak, pokud je křížení směrem dolů, je to prodejní signál.
- Lze použít tři klouzavé průměry. Ten, který zahrnuje více období, slouží jako filtr, tj. pro otevření nákupní pozice (býčí), musí být tento dlouhodobý průměr pod ostatními dvěma. Stejně tak pro otevření prodejní pozice (medvědí) musí být dlouhodobý průměr nad ostatními.
Aplikace strategie na reálných příkladech
Nyní se podívejme na případy, kde aplikujeme dvě z vysvětlených strategií: křížení ceny přes průměr a křížení průměrů. Je třeba poznamenat, že klouzavé průměry lze dále optimalizovat tak, že vysledujete počet sezení, který je pro dosažení vyšší ziskovosti nejlepší. Pokud vám přijde tato metoda složitá, možná vás nadchne copy trading. Pokud začínáte s investováním od nuly, pak se podívejte na našeho kompletního průvodce pro začátečníky.
1. Cena kříží klouzavý průměr (červená čára je klouzavý průměr a černá barva představuje cenové pohyby)

Na grafu můžeme vidět příklad, jaké operace by se prováděly v případě, že bychom sledovali strategii "cena kříží jednoduchý klouzavý průměr za 20 období". Zeleně vidíme signály k nákupu a červeně signály k prodeji nebo otevření krátkých pozic. Můžeme ověřit, že když je trh v bočním trendu, nabízí mnoho chybných signálů, ale když je v jasném trendu, operace vyjde dobře.
Pozor. Když klouzavý průměr začíná ztrácet sklon a stává se plochým, naznačuje nám to, že se trend vyčerpává.
2. Křížení klouzavých průměrů

V příkladu vidíme křížení exponenciálního klouzavého průměru za 13 období (tmavě modrá) a klouzavého průměru za 70 období (červená). Můžeme vidět, jak dlouhodobá strategie může být úspěšná s křížením průměrů, protože se vyhne mnoha falešným signálům. Strategie by byla koupit, když modrý klouzavý průměr překříží červený klouzavý průměr zdola nahoru, a prodat, když modrý klouzavý průměr překříží červený klouzavý průměr shora dolů.
3. Podpory a rezistence s klouzavými průměry
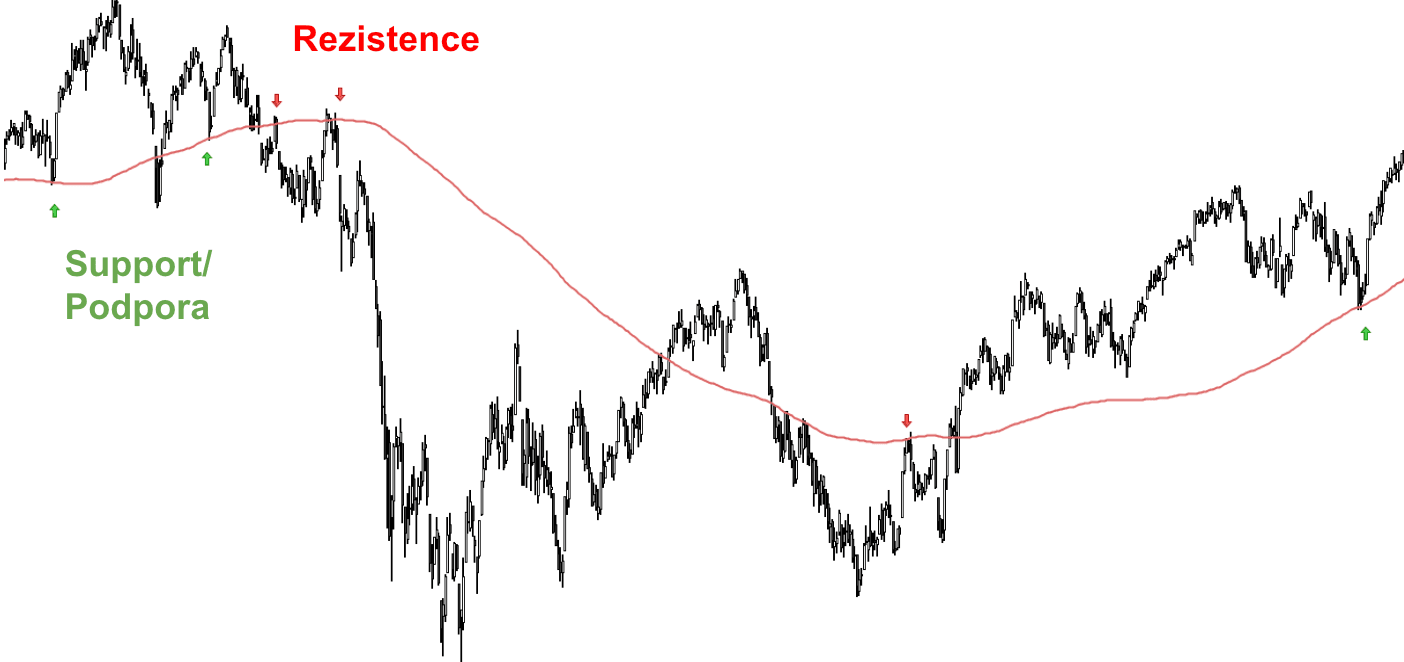
Na grafu můžeme pozorovat, jak nám jednoduchý klouzavý průměr za 200 období také ukazuje některé podpory (zelená šipka) a rezistence (červená šipka).
Výhody a nevýhody klouzavých průměrů:
| Výhody klouzavých průměrů: | Nevýhody klouzavých průměrů: | ||
| Jsou relativně snadno vypočítatelné (u všech tří typů se jedná o průměry). | Ukazují trend, ale ne jeho původ, nevíme důvody, proč se aktivum pohybuje. | ||
| Pomáhají identifikovat okamžiky nákupu a prodeje. | Pro dlouhodobé horizonty jsou některé nástroje vhodnější, např. fundamentální analýza. | ||
| Umožňují analytikovi zvolit počet pozorování, která budou použita k výpočtu průměru. | Je to zpožděný indikátor, to znamená, že ukazuje začátek nebo změnu trendu, ale neumožňuje jej předvídat. | ||
| Dovolují kombinovat různé strategie tradingu. | Klouzavé průměry jsou dobrými indikátory trendu, ale v bočních trendech poskytují velké množství chybných a protichůdných signálů. |
| Výhody klouzavých průměrů: | Nevýhody klouzavých průměrů: |
| Jsou relativně snadno vypočítatelné (u všech tří typů se jedná o průměry). | Ukazují trend, ale ne jeho původ, nevíme důvody, proč se aktivum pohybuje. |
| Pomáhají identifikovat okamžiky nákupu a prodeje. | Pro dlouhodobé horizonty jsou některé nástroje vhodnější, např. fundamentální analýza. |
| Umožňují analytikovi zvolit počet pozorování, která budou použita k výpočtu průměru. | Je to zpožděný indikátor, to znamená, že ukazuje začátek nebo změnu trendu, ale neumožňuje jej předvídat. |
| Dovolují kombinovat různé strategie tradingu. | Klouzavé průměry jsou dobrými indikátory trendu, ale v bočních trendech poskytují velké množství chybných a protichůdných signálů. |
Příklad klouzavého průměru
Podívejme se na jednoduchý příklad výpočtu tří typů klouzavých průměrů:
| Cena akcie X | Exponenciální klouzavý průměr | Jednoduchý klouzavý průměr | Vážený klouzavý průměr | ||||
| 6.97 | |||||||
| 5.94 | |||||||
| 5.73 | |||||||
| 5.73 | |||||||
| 5.61 | 6.00 | 6.00 | 5.80 | ||||
| 5.61 | 5.87 | 5.72 | 5.67 | ||||
| 6.78 | 6.17 | 5.89 | 6.02 | ||||
| 5.21 | 5.85 | 5.79 | 5.79 | ||||
| 5.17 | 5.62 | 5.67 | 5.59 | ||||
| 5.22 | 5.49 | 5.60 | 5.44 | ||||
| 6.83 | 5.94 | 5.84 | 5.85 | ||||
| 5.96 | 5.94 | 5.68 | 5.89 | ||||
| 6.44 | 6,11 | 5.92 | 6.14 | ||||
| 5.13 | 5.78 | 5.92 | 5.88 | ||||
| 6.91 | 6.16 | 6.25 | 6.21 | ||||
| 6.24 | 6.19 | 6.14 | 6.20 | ||||
| 6.80 | 6.39 | 6.31 | 6.43 | ||||
| 5.06 | 5.95 | 6.03 | 6.01 | ||||
| 6.91 | 6.27 | 6.38 | 6.31 | ||||
| 5.06 | 5.87 | 6.01 | 5.86 |
| Cena akcie X | Exponenciální klouzavý průměr | Jednoduchý klouzavý průměr | Vážený klouzavý průměr |
| 6.97 | |||
| 5.94 | |||
| 5.73 | |||
| 5.73 | |||
| 5.61 | 6.00 | 6.00 | 5.80 |
| 5.61 | 5.87 | 5.72 | 5.67 |
| 6.78 | 6.17 | 5.89 | 6.02 |
| 5.21 | 5.85 | 5.79 | 5.79 |
| 5.17 | 5.62 | 5.67 | 5.59 |
| 5.22 | 5.49 | 5.60 | 5.44 |
| 6.83 | 5.94 | 5.84 | 5.85 |
| 5.96 | 5.94 | 5.68 | 5.89 |
| 6.44 | 6,11 | 5.92 | 6.14 |
| 5.13 | 5.78 | 5.92 | 5.88 |
| 6.91 | 6.16 | 6.25 | 6.21 |
| 6.24 | 6.19 | 6.14 | 6.20 |
| 6.80 | 6.39 | 6.31 | 6.43 |
| 5.06 | 5.95 | 6.03 | 6.01 |
| 6.91 | 6.27 | 6.38 | 6.31 |
| 5.06 | 5.87 | 6.01 | 5.86 |
Máme tedy údaje o ceně aktiva během dvaceti období. Z důvodu praktičnosti budeme počítat klouzavé průměry pomocí pěti období.
Jednoduchý klouzavý průměr je aritmetický průměr, to znamená, součet hodnot dělený počtem dat. Příklad:
průměr za období 5= (6,97+5,94+5,73+5,73+5,61)/5=5,996=6,00
Pro výpočet EMA (exponenciální varianta) používáme jako první údaj jednoduchý klouzavý průměr. Pak se použije vyhlazovací faktor nazývaný k.
k=2/(1+p)=2/6=0,3333
*p je počet období, tedy 5 v příkladu.
Poté použijeme vzorec:
EMA za období 6 = cena za období 6 * k + EMA za období 5 * (1-k)
EMA za období 6= 5,61*0,3333+6*(1-0,3333)=5,87
Na závěr, pro vážený klouzavý průměr, se každé datum násobí číslem mezi 1 a 5, přičemž se nejvzdálenější období násobí 1 a nejbližší 5. Poté se dělí 15 (součet čísel od 1 do 5).
Příklad:
(1*6,97+2*5,94+3*5,73+4*5,73+5*5,61)/15=5,80
