Fisherova rovnice a inflace

Irving Fisher je americký ekonom, podle kterého je pojmenována Fisherova rovnice – ekonomická rovnice vysvětlující vztah mezi úrokovými sazbami a inflací.

Konkrétněji, Fisherova rovnice stanovuje, prostřednictvím rovnosti, způsob, jakým se vztahuje úroková sazba, jak nominální, tak reálná, a očekávaná inflace. Rovnice je následující:

To znamená, že Fisherova rovnice uzavírá, že pro určení reálné úrokové sazby pro půjčku (například) bude nutné odečíst očekávanou míru inflace od předpokládané nominální úrokové sazby.

Například, pokud věřitelé požadují reálnou úrokovou sazbu 3 %, ale zároveň se očekává inflace 2 %, v této situaci a podle Fisherovy rovnice bude nominální úroková sazba 5 %.

Z analýzy této rovnice vyplývá jev známý jako Fisherův efekt: zvýšení míry inflace se přenáší jeden k jednomu na nominální úrokovou sazbu.

Jaký je rozdíl mezi reálnou a nominální úrokovou sazbou?

Pro správné pochopení Fisherovy rovnice je nutné provést krátký popis obou typů úrokových sazeb. Nominální úroková sazba je ta, která ukazuje výnos operace jako rozdíl mezi dvěma cenami.

Naopak, reálná úroková sazba bere v úvahu možnou změnu kupní síly peněz, to znamená, že bere v úvahu inflaci. Proto v Fisherově rovnici nominální úroková sazba zahrnuje, nebo ještě nebyla odečtena, míra inflace.

Proč je Fisherova rovnice užitečná pro vysvětlení úrokových sazeb?

Pokud se podíváme na trendy inflace v posledních letech, dospějeme k závěru, že Fisherova rovnice platí, protože vývoj těchto dvou údajů šel ruku v ruce. To znamená, že když je inflace vysoká, nominální úrokové sazby mají tendenci být vysoké a když je nízká, mají tendenci být nízké.

Tento úzký vztah mezi oběma sazbami lze ověřit v různých zemích, což poskytuje další argumenty pro tvrzení, že Fisherova rovnice je vzorec, který je třeba brát v úvahu, pokud chceme správně předpovědět chování úrokových sazeb.

Na následujícím grafu můžeme vidět případ USA, kde porovnáváme nominální úrokovou sazbu tříměsíčních pokladničních poukázek s inflací, pomocí přibližných dat, trend, který následovaly, a jak jsou obě proměnné úzce propojeny:

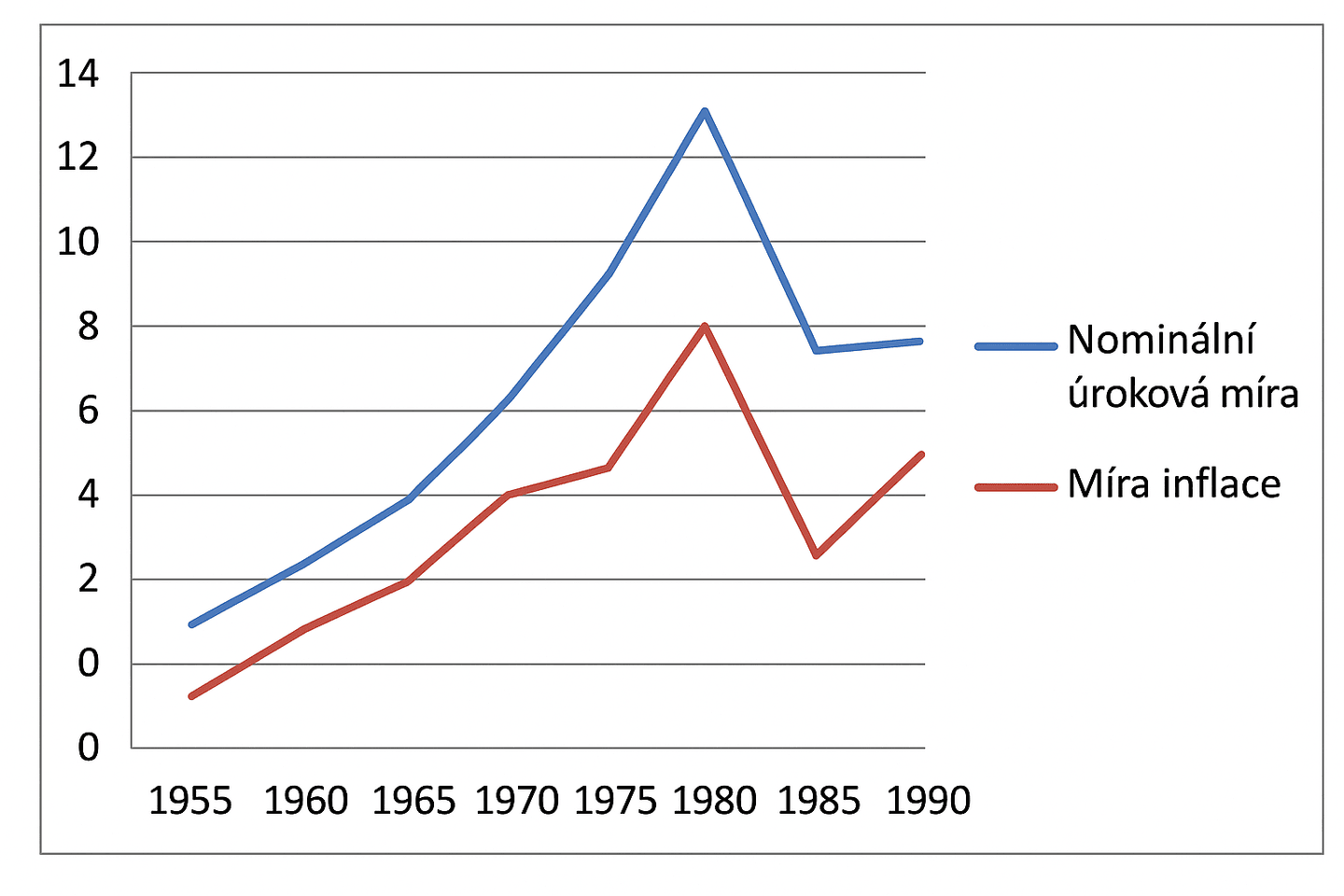
Fisherova rovnice je také ceněna mnoha investory na burze, protože ceny dluhopisů se mění nepřímo úměrně úrokovým sazbám. Tímto způsobem, pokud správně předpovíme vývoj úrokových sazeb, naše výnosy z burzovních investic mohou vzrůst. Důkazem toho je, že společnosti na Wall Street najímají profesionály, kteří sledují pohyby měnové politiky a inflace, aby lépe předpověděli úrokové sazby.

Pochopení Fisherovy rovnice

Pro lepší pochopení Fisherovy rovnice si můžeme ukázat dva příklady. Nejprve osoba, která si bere půjčku. Použijeme nereálnou situaci, ale je to pro zjednodušení analýzy. Předpokládejme, že Jan si vezme půjčku 1.000 eur a za to koupí 1.000 banánů, protože každý banán stojí 1 euro.

Nyní je úroková sazba půjčky 5 %, takže na konci by musel vrátit 1.050 eur, přičemž úroky činí 50 eur (1.000*5 %).

Během stejného období zadlužení předpokládejme, že očekávaná inflace je 2 %. Proto banány již nebudou stát 1 euro, ale 1,02 eura každý.

Co se stane na konci období financování? Pokud bychom banány prodali, vydělali bychom 1.020 eur (1.000*0,02). To znamená, že zisk by byl 20 eur. Ale zároveň jsem zaplatil úroky ve výši 50 eur. Proto v reálných termínech je náklad na zadlužení 30 eur (50-20).

Kolik těchto 30 eur odpovídá v banánech? Rozdělíme 30 cenou konečného banánu (1,02 eura), což dává výsledek 29,41 banánů. Takže z půjčky na nákup 1.000 banánů zaplatíme 29,41 banánů. To znamená, že reálná úroková sazba je 29,41 z 1.000, což je rovno 2,94 % (29,41/1.000). Tato sazba je nižší než nominální úroková sazba (5 %).

Můžeme tedy pozorovat, že Fisherova rovnice platí, protože nominální úroková sazba (5 %) je přibližně rovna reálné úrokové sazbě (2,94 %) plus inflaci (2 %).

Jiný způsob vyjádření Fisherovy rovnice

Nyní uvidíme další příklad, jak lze analyzovat Fisherovu rovnici z jiného úhlu pohledu. Představíme si situaci z pohledu věřitelky, kterou nazveme Jana. Má 12 000 eur, které může ušetřit nebo půjčit.

Pokud je půjčí, je ochotna přijmout roční úrokovou sazbu 6 %. Nyní by její alternativou mohlo být nakoupit zboží, například židle, a poté je prodat za vyšší cenu, která bude záviset na inflaci.

Předpokládejme, že roční inflace byla 4 % a Viktorie půjčila 12 000 eur s ročním úrokem 6 %. Jaký byl skutečný výnos poskytnuté půjčky?

Pro výpočet pokračujme s příkladem židlí, abychom zjednodušili analýzu. V době poskytnutí půjčky byla jejich cena 5 eur. S inflací (4 %) vzrostla na 5,2 eur (5*1,04).

Nyní vypočítáme skutečnou návratnost nebo výnos Viktorie (1+r), jako u jakékoli investice, dělením konečné hodnoty počáteční investicí.

Konečná hodnota je půjčená částka plus úroky (1+i), ale vyjádříme ji v počtu židlí, dělením cenou židlí v době ukončení půjčky (5,2 eur), kterou nazveme konečná cena nebo pf. Máme následující:

konečná hodnota = (1+i)/pf

Jaká by tedy byla počáteční investice? Abychom to vyjádřili také v počtu židlí, musíme půjčenou částku vydělit cenou zboží v čase 0, tedy 5 eur, kterou nazveme počáteční cena nebo pi.

Protože nás zajímá výnos na každý půjčený euro, dělíme pouze 1 pi.

Počáteční investice 1/pi

Vzorec by vypadal takto:

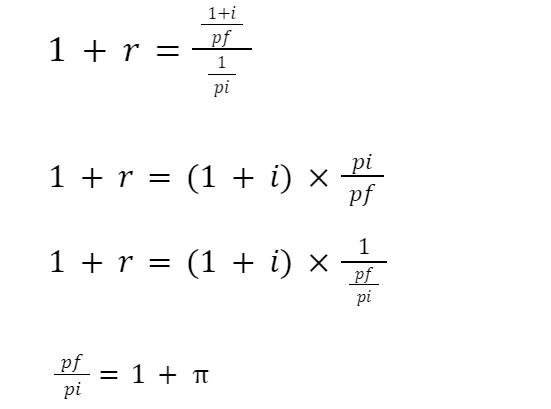
Proto:

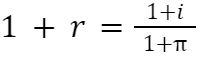
S tímto vzorcem, vracejíc se k příkladu Viktorie, je výnos poskytnuté půjčky:

1+r=(1+0.06)/(1+0.04)=1.06/1.04
1+r=1.0192
r=0.0192
r=1.92%

Můžeme znovu konstatovat, že skutečný úrok nebo výnos (1,92 %) je nižší než nominální (6 %) a rozdíl je dán inflací (4 %).

Pokud věnujeme více pozornosti, uvědomíme si také, že pokud je míra inflace vyšší než úroková sazba poskytnuté půjčky, například 8 %, je výnos pro Viktorii záporný.

1+r=(1+0.06)/(1+0.08)=1.06/1.08=0.9815
1+r=0.9815
r=-0.0185
r=-1.85%

Jak se tento výsledek vysvětluje? Ukazuje se, že by pro Viktorii bylo výhodnější, místo poskytnutí půjčky, koupit židle a poté je prodat za vyšší cenu.

Židle již nezdražily z 5 na 5,2 eura, ale na 5,4 eura. Proto za 12.000 eur, které měla půjčit, koupí 2.400 židlí (12.000/5) a poté je prodá za 5,4 eura každou, což činí celkem 12.960 (2.400*5,4). Zisk byl 960 eur (12.960-12.000). Naopak, pokud poskytne půjčku, vydělá pouze 6 % z 12.000, tedy 720 (12.000*0,06).

Z výše uvedeného můžeme odvodit, že pokud Victoria očekává vyšší míru inflace, bude také požadovat vyšší nominální úrok za poskytnutou půjčku. Jinak bude její výnos záporný. To vysvětluje, z jiného úhlu pohledu, vztah mezi třemi proměnnými, které tvoří Fisherovu rovnici.