Indikátory
Fibonacciho posloupnost: interpretace a příklady využití při tradingu

Fibonacciho posloupnost je fascinující číselný vzorec, který po staletí udivuje matematiky, obchodníky a analytiky. Tato sekvence, odvozená z jednoduchého souboru pravidel, má hluboké spojení s různými aspekty života a bylo zjištěno, že má pozoruhodné uplatnění také na finančních trzích.
V tomto článku prozkoumáme význam Fibonacciho čísel ve světě financí. Vysvětlíme, jak tradeři používají Fibonacciho nástroje, jako jsou Fibonacciho retracements, expanze, vějíře a časové zóny. Podíváme se, jak identifikovat klíčové úrovně, předpovědět potenciální cenové pohyby a tržní trendy v rámci technické analýzy.

Historie Leonarda Fibonacciho z Pisy
Leonardo Fibonacci z Pisy, známý spíše pod přezdívkou Fibonacci, se narodil v italském městě Pisa. Žil v letech 1170 až 1250. Říkal si „Bigollo“, což znamená „k ničemu".
Leonardo začíná formovat svou identitu obchodníka a matematika ve městě Bugia (nyní Bejaia), což je přístavní město na severovýchodě Alžírska.
O jeho životě se toho ví jen velmi málo. Nicméně v předmluvě jedné ze svých nejvýznamnějších knih (Liber Abaci) Leonardo zdůrazňuje, že to byl jeho otec, kdo ho učil aritmetiku a povzbuzoval ho ke studiu matematiky.
V Bugii Leonarda učili arabští instruktoři, což byla pro mladého středověkého Itala, který se toužil naučit matematiku ta nejlepší zkušenost. Specializoval se na aritmetiku a různé číselné systémy používané v té době. Po krátké době se Leonardo sám přesvědčil o výjimečnosti indoarabského systému oproti různým zemím, které navštívil. Rozhodl se zavést tento systém v Itálii a v ideálním případě i po celé Evropě, kde stále převládaly římské číslice a počítadla.
Studium matematiky a její praktické aplikace jako nepostradatelného nástroje pro rozvoj obchodu zabralo značnou část Fibonacciho života.

Leonardo Fibonacci a matematika
Leonardo se vrátil do Pisy kolem roku 1200, kde napsal řadu knih a textů o matematice. Za jeho doby ještě nebyl vynalezen tiskařský stroj, takže jeho díla byla psána ručně a kolované kopie se také přepisovaly precizně ručně.
Snadno si můžeme představit omezený počet kopií, které v té době mohly po světě kolovat. Nicméně, přestože se to zdá málo pravděpodobné, několik knih se podařilo dochovat až do dnešních dnů (včetně Liber Abaci z roku 1202, Practica Geometriae z roku 1220, Flos z 1225 nebo Liber Quadratorum napsané v roce 1227). Bohužel, spoustu dalších děl se během historie ztratilo nebo se nepodařilo zachránit.
V roce 1200 Fibonacci publikoval svou proslulou Liber Abaci, která do Evropy přivedla jeden z nejvýznamnějších matematických nástrojů v celé historii — desítkovou číselnou soustavu. Tato kniha představila základní aritmetické operace ve formě celých čísel a zlomků. Také se zabývala pokročilou trigonometrií a algebrou arabských učenců. Jednalo se o tak významný průlom v matematice, že Fibonacciho zjištění a objevy zůstaly srovnávacím měřítkem v celém západním světě po další tři století.
Časem Leonardova reputace stále stoupala a v roce 1225 byl široce uznáván jako jeden z nejlepších matematiků. Dokonce soudy a nejrůznější podniky žádaly o jeho rady.
Fibonacciho posloupnost
Fibonacciho posloupnost uvedená v Liber Abaci představuje výzvu pro výpočet růstu králičí populace od jejího počátečního stavu. K vyřešení tohoto problému Fibonacci navrhuje následující řešení.
Začínáme se dvěma králíky (pár A), kteří se rozmnoží a ve druhém měsíci porodí pár samce a samice (pár B). Následně máme dva páry králíků. Kromě toho se ve druhém měsíci původní pár ještě jednou rozmnoží a zplodí nový pár potomků (pár C), kteří se narodí ve třetím měsíci. Navíc během třetího měsíce pár B vstoupí do reprodukční fáze a ve čtvrtém měsíci porodí další pár králíků (pár D). Stejně tak má pár A třetí vrh (pár E). Vždy se předpokládá, že když se králíci rozmnožují, přivedou na svět pár, který se na konci prvního měsíce života stává také plodným.
Za těchto předpokladů Leonardo řeší problém zavedením rekurentního vztahu, který byl později na jeho počest pojmenován jako Fibonacciho posloupnost. Je prezentován jako řešení matematického problému týkajícího se rychlosti rozmnožování králíků za specifických okolností.
Fibonacciho posloupnost nebo sekvence se tedy vypočítá tak, že přičtete aktuální číslo k číslu předchozímu: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 atd.
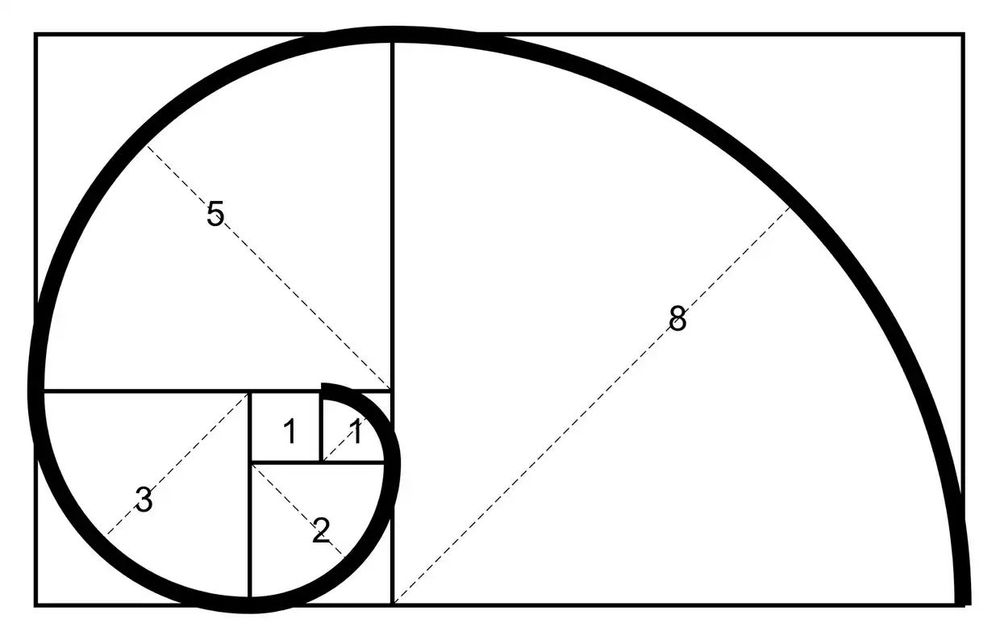
Vlastnosti Fibonacciho posloupnosti
- Fibonacciho posloupnost je řada čísel, kde každé číslo je součtem dvou čísel předchozích.
- Poměr mezi číslem a jeho předchůdcem (tn/tn-1) se blíží zlatému řezu Phi, který se přibližně rovná ≈ 1,618. Podobně poměr mezi číslem a následujícím číslem (tn-1/tn) má tendenci se blížit převrácené hodnotě Phi, což je přibližně 0,618. Tyto vztahy platí pro většinu čísel ve Fibonacciho posloupnosti, kromě prvních tří čísel.
- Další zajímavou vlastností Fibonacciho posloupnosti je, že součet prvních deseti členů se rovná jedenáctinásobku jejího sedmého člene. Tato vlastnost platí pro jakoukoli řadu vytvořenou podle předpokladů Fibonacciho posloupnosti, bez ohledu na výběr počátečních dvou čísel.
- Dále, pokud vezmeme jakékoli číslo ze sekvence počínaje 3. členem, vynásobíme ho 4 a pak toto číslo přičteme k číslu, které stojí tři pozice před ním, získáme číslo umístěné tři pozice za tímto číslem. To můžeme algebraicky vyjádřit jako tn*4 + tn-3 = tn+3. Pokud například vezmeme v úvahu posloupnost: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 a vezmeme číslo 21, vynásobíme ho 4 a přidáme číslo 5 (což jsou tři pozice před 21), pak získáme číslo 89 (které se nachází 3 pozice za tímto číslem).
Fibonacciho posloupnost v technické analýze
Fibonacciho posloupnost se často používá v technické analýze. Z této posloupnosti jsou odvozeny některé nástroje. Tyto nástroje používají poměr mezi různými číslicemi v řade, hlavně mezi daným číslem a číslem předchozím. Čím vyšší jsou tyto poměry, tím více se výsledek blíží zlatému řezu (1,618). Rovnice zlatého řezu je:
Zlatý řez je ve zkratce jedno jediné: poměr o hodnotě zhruba 1,62. Zlatý řez je matematický poměr, který je definován jako poměr dvou čísel, přičemž poměr většího k menšímu je stejný jako poměr jejich součtu k většímu z nich. Tento poměr se často označuje jako fyzikální konstanta Phi (Φ) a má přibližnou hodnotu právě 1,6180339887...
Na základě tohoto zlatého řezu vzniká řada proporcí, které vykazují přímý matematický vztah s touto hodnotou. Tyto proporce lze použít v technické analýze při analýze grafů.
| Hlavní proporce | |
| 0.236 | |
| 0.382 | |
| 0.5 | |
| 0.618 | |
| 0.746 | |
| 1 | |
| 1.382 | |
| 1.618 | |
| 2.618 | |
| 4.618 |
| Hlavní proporce |
| 0.236 |
| 0.382 |
| 0.5 |
| 0.618 |
| 0.746 |
| 1 |
| 1.382 |
| 1.618 |
| 2.618 |
| 4.618 |
Technická analýza a Fibonacciho nástroje
Fibonacciho časové zóny
Fibonacciho časové zóny (nebo Fibonacciho časová pásma) jsou technickým analytickým nástrojem, který vychází z Fibonacciho posloupnosti. Používají se k identifikaci potenciálních bodů obratu nebo pokračování trednu.
Obvykle se používají počítáním od významného vrcholu nebo dna na grafu k dalšímu významnému nejvyššímu nebo nejnižšímu bodu. Čáry vyznačené na grafu jsou interpretovány jako potenciální inflexní body v budoucnu čili body, kde může dojít k obratu trendu.
Na denním grafu se Fibonacciho obchodní dny počítají pomocí čísel z Fibonacciho posloupnosti, jako je 5, 8, 13, 21, 34 atd. Mnoho platforem pro tvorbu grafů však má vestavěné nástroje, které automaticky zobrazují Fibonacciho časové zóny, což eliminuje potřebu manuálního počítání. Stojí za zmínku, že účinnost Fibonacciho časových zón může na kratších časových grafech kolísat a klesat.
Fibonacciho vějíře
Fibonacciho vějíře jsou dalším nástrojem široce používaným v technické analýze. Pomáhají identifikovat potenciální úrovně supportu a rezistence (podpory a odporu) a poskytují vhled do načasování a hloubky korekcí po impulzním pohybu. Při použití Fibonacciho vějířů se čára táhne od nejnižší hodnoty k nejvyšší hodnotě impulzního pohybu.
Nástroj pak vygeneruje řadu čar s různými úhly sklonu na základě důležitých Fibonacciho poměrů. Pokud je hlavní impulz býčí, Fibonacciho vějíře se kreslí od minima k maximu. Pokud je hlavní impulz medvědí, kreslí se naopak od maxima k minimu.
Fibonacciho expanze
Fibonacciho expanze (neboli rozšíření) je nástroj používaný v technické analýze k projektování potenciálních cenových cílů nebo úrovní expanze v probíhajícím trendu. Na rozdíl od ostatních Fibonacciho nástrojů vyžaduje jak počáteční impulz, tak korekční pohyb. Účelem Fibonacciho expanze je odhadnout, jak daleko může impulzní vlna pokračovat.
Pro vykreslení Fibonacciho expanze se kurzor umístí na základnu impulzní vlny. Poté se přesune na vrchol první vnitřní podvlny v rámci korekční fáze. Následně se kurzor vrátí zpět na základnu druhé vnitřní podvlny. Nástroj pak generuje různé Fibonacciho proporční čáry, které indikují potenciální úrovně, na které by se mohla impulzní vlna rozšířit.
Tyto Fibonacciho proporční čáry poskytují obchodníkům potenciální cenové cíle nebo oblasti zájmu, kde byl mohl trend narazit na významnou rezistenci nebo support. Projektováním těchto úrovní mohou obchodníci odhadnout potenciální sílu a dobu trvání probíhajícího trendu.
Fibonacciho retracementy
Fibonacciho retracementy jsou jedním z nejpoužívanějších nástrojů odvozených z Fibonacciho posloupnosti v rámci technické analýzy. Tento nástroj se používá k identifikaci potenciálních oblastí, kde může korekční pohyb najít úroveň supportu nebo rezistence. Pro efektivní použití Fibonacciho retracementů je nutné mít dokončený předchozí impulzní pohyb. Bez předchozího impulzu nemusí nástroj poskytovat užitečné informace.
Pro správnou aplikaci Fibonacciho retracementů musíme identifikovat nejnižší a nejvyšší body dokončeného impulzu a na základě těchto bodů nakreslit úrovně retracementu. Standardně jsou na grafu označeny výchozí úrovně 23,6%, 38,2%, 50% a 61,8%, přičemž poslední je ekvivalentem zlatého řezu.
Podle této teorie je nejpravděpodobnější zóna pro ukončení korekčního procesu mezi úrovněmi 50 % a 61,8 % retracementu. Tyto úrovně jsou často považovány za oblasti, kde může cena najít support nebo rezistenci před obnovením hlavního trendu. V případě korekce směrem nahoru po medvědím impulzu může například cena najít potenciální bod obratu kolem 50 % úrovně retracementu a pokračovat v medvědím trendu.
Interpretace Fibonacciho čísel a linií při tradingu
Někteří tradeři považují Fibonacciho čísla za zásadně důležitá. Fibonacciho číselnou posloupnost lze použít k vytvoření poměrů nebo procent, které tradeři běžně používají, jako jsou 23,6 %, 38,2 %, 50 %, 61,8 %, 78,6 %, 100 %, 161,8 %, 261,8 % a 423,6 %.
Tato procenta se používají při různých technikách, například:
- Fibonacciho retracementy: vodorovné linie na grafu označující oblasti supportu a rezistence.
- Fibonacciho expanze: vodorovné linie na grafu označující cenové úrovně, kam by potenciálně mohla dosáhnout silná vlna nebo trend.
- Fibonacciho oblouky: zakřivené čáry odvozené od významného vrcholu nebo dna, které představují oblasti potenciálního supportu a rezistence.
- Fibonacciho vějíře: diagonální linie generované pomocí významného vrcholu nebo dna k identifikaci oblastí potenciálního supportu a rezistence.
- Fibonacciho časové zóny: svislé čáry na grafu sahající do budoucnosti, předpovídají potenciální časová období pro významné cenové pohyby.
Mezi těmito technikami jsou Fibonacciho retracementy nejběžněji používanou formou technické analýzy založené na Fibonacciho posloupnosti. Tradeři tento nástroj používají k určení potenciální úrovně retracementu nebo korekce v kontextu současného trendu.
Fibonacciho posloupnost: Shrnutí
Využití Fibonacciho posloupnosti v technické analýze a tradingu nabízí traderům mocný nástroj pro identifikaci klíčových cenových úrovní a potenciálních bodů obratu na trzích. Pomáhá jim lépe porozumět dynamice trhu a zlepšit přesnost svých obchodních rozhodnutí. Při správném využití může Fibonacciho posloupnost posílit obchodní strategie a přispět k úspěšnému obchodování na finančních trzích.
Závěrem je důležité poznamenat, že Fibonacciho matematická koncepce nebyla původně vytvořena pro obchodní účely. Tradeři a analytici Fibonacciho nástroje používají jednoduše proto, že jim poskytují strukturovaný rámec pro efektivnější vyhodnocení obchodních příležitostí.
Dozvědět se více o tradingu a technické analýze: