Akciový trh
Co je kovariance
Kovariance je míra vztahu mezi dvěma náhodnými proměnnými. Pokud proměnné nejsou propojené, kovariance bude nula.
Jinými slovy, kovariance se snaží měřit, do jaké míry dvě proměnné společně kolísají, ať už ve stejném směru nebo s opačnými pohyby.
Vzorec pro kovarianci
Pro vzorec kovariance nejprve vezmeme dvě proměnné, x a y. Poté následujeme následující rovnici:
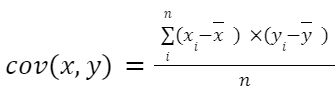
V rovnici x a y s vodorovnou čarou nahoře představují aritmetický průměr datové sady. Stejně tak n je počet pozorování.
Pokud máme tabulku frekvencí se seskupenými daty, vzorec by byl:
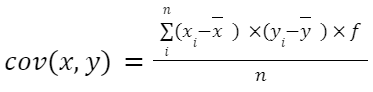
Kde f je frekvence, tedy počet opakování pozorování, jak v x, tak v jeho odpovídajícím y (bude jasnější s příkladem později).
Vlastnosti kovariance
Některé vlastnosti kovariance jsou:
- Kovariance mezi proměnnou a konstantou je nula.
- Kovariance mezi proměnnou a jí samotnou je rozptyl této proměnné.
- Když je kovariance kladná, obě proměnné se pohybují stejným směrem, to znamená, že pokud x stoupá, y také stoupá. Ale pokud je kovariance záporná, proměnné mají inverzní vztah, když jedna stoupá, druhá klesá a naopak.
- Pokud je kovariance nula, proměnné nemají mezi sebou vztah.
- Když se změní jednotka měření proměnných, například z gramů na kilogramy, výsledek kovariance se také změní. Pamatujme, že se nejedná o normalizovanou míru, což ztěžuje srovnání mezi kovariancemi.
Aplikace kovariance
Některé z hlavních aplikací kovariance při rozhodování o investicích jsou:
- Měření rizika: Kovariance umožňuje měřit riziko investice do aktiva nebo portfolia aktiv. Vysoká kovariance naznačuje vysoké riziko, zatímco nízká kovariance naznačuje nízké riziko.
- Hodnocení diverzifikace: Kovariance také umožňuje hodnotit diverzifikaci portfolia aktiv. Vysoce diverzifikované portfolio bude mít nízkou kovarianci, což naznačuje nízké riziko. Proto může kovariance pomoci investorům vybrat aktiva, která se vzájemně doplňují, a snížit riziko portfolia.
- Určení očekávané výnosnosti: Kovariance se také používá k určení očekávané výnosnosti portfolia aktiv. Očekávaná výnosnost se vypočítá jako součin kovariance mezi výnosem každého aktiva a jeho váhou v portfoliu. Tyto informace mohou pomoci investorům rozhodnout, která aktiva zahrnout do svého portfolia a v jakém poměru.
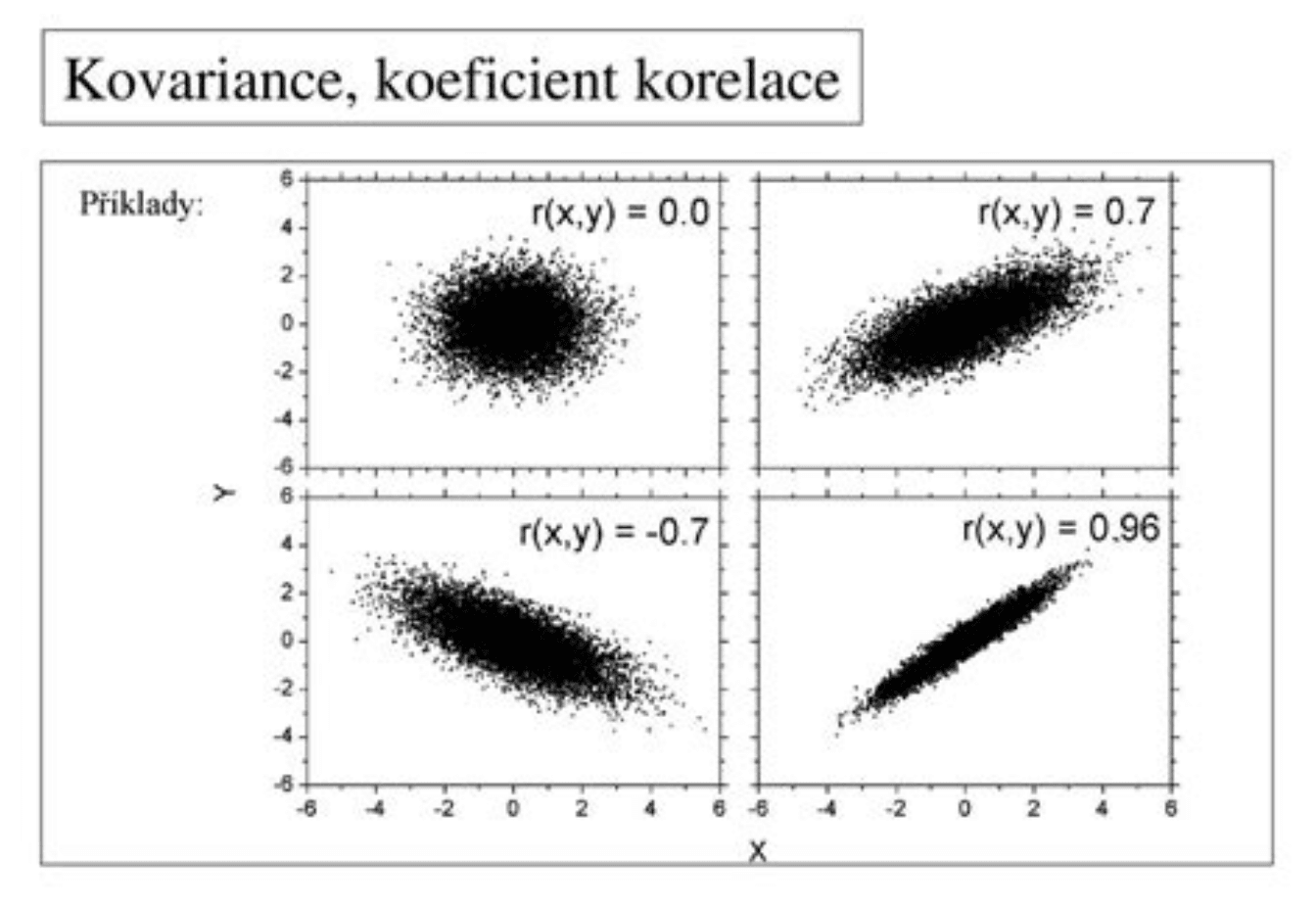
Kovariance a korelace
Kovariance a korelace jsou dva pojmy, které souvisejí s rizikem a diverzifikací v investování, ale mají určité rozdíly.
Kovariance je míra vztahu mezi dvěma proměnnými, zatímco korelace je normalizovaná míra tohoto vztahu. Kovariance se vypočítá násobením rozdílů mezi hodnotami každé proměnné a jejich příslušným průměrem a následným dělením výsledku počtem dat. To nám dává představu o tom, jak se dvě proměnné mění společně, ale neříká nám nic o tom, jak silný je tento vztah.
Na druhou stranu, korelace se vypočítá dělením kovariance součinem standardních odchylek obou proměnných. To nám dává normalizovanou míru vztahu mezi dvěma proměnnými, což nám umožňuje snadno porovnat sílu tohoto vztahu s jinými vztahy mezi proměnnými. Korelace se vyjadřuje jako číslo mezi -1 a 1, kde hodnota 1 označuje dokonale pozitivní korelaci, hodnota -1 označuje dokonale negativní korelaci a hodnota 0 označuje, že mezi proměnnými není žádná korelace.
Praktické aplikace výpočtu kovariance
Například, pokud se měří váha a výška osoby v pravidelných intervalech během jejího života, lze vypočítat kovarianci mezi váhou a výškou v každém okamžiku. To by vám poskytlo míru toho, jak úzce jsou váha a výška korelovány v průběhu času. Pokud by byly dokonale korelovány, kovariance by byla 1. Pokud by nebyly vůbec korelovány, byla by 0.
Příklad ze světa investic, pokud chcete vědět, jak si vede akciový trh, můžete se podívat na Dow Jones Industrial Average (DJIA) a S&P 500. DJIA měří vývoj cen akcií 30 velkých společností, zatímco S&P 500 měří vývoj cen akcií 500 velkých společností. Pokud bychom chtěli vědět, jak si vede akciový trh, vypočítali bychom kovarianci mezi těmito dvěma datovými soubory. To by vám řeklo, jak moc se každý datový soubor pohybuje ve vztahu k druhému.
Prakticky to znamená, že zjistíme, jestli se hodnoty obou indexů (DJIA a S&P 500) mění podobně – tedy jestli když jeden roste, roste i druhý, a když jeden klesá, klesá i ten druhý.
Příklad:
Předpokládejme, že máme dvě proměnné, x a y, s 32 pozorováními každé
| X | Y | ||||
| 1 | 10 | 5 | |||
| 2 | 5 | 10 | |||
| 3 | 3 | 3 | |||
| 4 | 10 | 8 | |||
| 5 | 10 | 9 | |||
| 6 | 8 | 1 | |||
| 7 | 8 | 8 | |||
| 8 | 5 | 1 | |||
| 9 | 1 | 2 | |||
| 10 | 8 | 4 | |||
| 11 | 9 | 1 | |||
| 12 | 4 | 7 | |||
| 13 | 8 | 5 | |||
| 14 | 8 | 7 | |||
| 15 | 6 | 4 | |||
| 16 | 3 | 4 | |||
| 17 | 5 | 8 | |||
| 18 | 4 | 2 | |||
| 19 | 10 | 1 | |||
| 20 | 2 | 1 | |||
| 21 | 1 | 6 | |||
| 22 | 3 | 8 | |||
| 23 | 8 | 9 | |||
| 24 | 3 | 1 | |||
| 25 | 3 | 10 | |||
| 26 | 8 | 7 | |||
| 27 | 5 | 3 | |||
| 28 | 9 | 1 | |||
| 29 | 7 | 5 | |||
| 30 | 5 | 4 | |||
| 31 | 9 | 6 | |||
| 32 | 8 | 8 | |||
| prům | 6,1250 | 4,9688 |
| X | Y | |
| 1 | 10 | 5 |
| 2 | 5 | 10 |
| 3 | 3 | 3 |
| 4 | 10 | 8 |
| 5 | 10 | 9 |
| 6 | 8 | 1 |
| 7 | 8 | 8 |
| 8 | 5 | 1 |
| 9 | 1 | 2 |
| 10 | 8 | 4 |
| 11 | 9 | 1 |
| 12 | 4 | 7 |
| 13 | 8 | 5 |
| 14 | 8 | 7 |
| 15 | 6 | 4 |
| 16 | 3 | 4 |
| 17 | 5 | 8 |
| 18 | 4 | 2 |
| 19 | 10 | 1 |
| 20 | 2 | 1 |
| 21 | 1 | 6 |
| 22 | 3 | 8 |
| 23 | 8 | 9 |
| 24 | 3 | 1 |
| 25 | 3 | 10 |
| 26 | 8 | 7 |
| 27 | 5 | 3 |
| 28 | 9 | 1 |
| 29 | 7 | 5 |
| 30 | 5 | 4 |
| 31 | 9 | 6 |
| 32 | 8 | 8 |
| prům | 6,1250 | 4,9688 |
Na konci tabulky jsme vypočítali průměry, abychom mohli aplikovat vzorec uvedený výše. Uděláme to krok za krokem.
Takto odečteme každé pozorování od průměru proměnné (x a y tučně), a oba výsledky vynásobíme.
| xi-x | yi-y | (xi-x)*(yi-y) | |||
| 3,8750 | 0,0313 | 0,1211 | |||
| -1,1250 | 5,0313 | -5,6602 | |||
| -3,1250 | -1,9688 | 6,1523 | |||
| 3,8750 | 3,0313 | 11,7461 | |||
| 3,8750 | 4,0313 | 15,6211 | |||
| 1,8750 | -3,9688 | -7,4414 | |||
| 1,8750 | 3,0313 | 5,6836 | |||
| -1,1250 | -3,9688 | 4,4648 | |||
| -5,1250 | -2,9688 | 15,2148 | |||
| 1,8750 | -0,9688 | -1,8164 | |||
| 2,8750 | -3,9688 | -11,4102 | |||
| -2,1250 | 2,0313 | -4,3164 | |||
| 1,8750 | 0,0313 | 0,0586 | |||
| 1,8750 | 2,0313 | 3,8086 | |||
| -0,1250 | -0,9688 | 0,1211 | |||
| -3,1250 | -0,9688 | 3,0273 | |||
| -1,1250 | 3,0313 | -3,4102 | |||
| -2,1250 | -2,9688 | 6,3086 | |||
| 3,8750 | -3,9688 | -15,3789 | |||
| -4,1250 | -3,9688 | 16,3711 | |||
| -5,1250 | 1,0313 | -5,2852 | |||
| -3,1250 | 3,0313 | -9,4727 | |||
| 1,8750 | 4,0313 | 7,5586 | |||
| -3,1250 | -3,9688 | 12,4023 | |||
| -3,1250 | 5,0313 | -15,7227 | |||
| 1,8750 | 2,0313 | 3,8086 | |||
| -1,1250 | -1,9688 | 2,2148 | |||
| 2,8750 | -3,9688 | -11,4102 | |||
| 0,8750 | 0,0313 | 0,0273 | |||
| -1,1250 | -0,9688 | 1,0898 | |||
| 2,8750 | 1,0313 | 2,9648 | |||
| 1,8750 | 3,0313 | 5,6836 |
| xi-x | yi-y | (xi-x)*(yi-y) |
| 3,8750 | 0,0313 | 0,1211 |
| -1,1250 | 5,0313 | -5,6602 |
| -3,1250 | -1,9688 | 6,1523 |
| 3,8750 | 3,0313 | 11,7461 |
| 3,8750 | 4,0313 | 15,6211 |
| 1,8750 | -3,9688 | -7,4414 |
| 1,8750 | 3,0313 | 5,6836 |
| -1,1250 | -3,9688 | 4,4648 |
| -5,1250 | -2,9688 | 15,2148 |
| 1,8750 | -0,9688 | -1,8164 |
| 2,8750 | -3,9688 | -11,4102 |
| -2,1250 | 2,0313 | -4,3164 |
| 1,8750 | 0,0313 | 0,0586 |
| 1,8750 | 2,0313 | 3,8086 |
| -0,1250 | -0,9688 | 0,1211 |
| -3,1250 | -0,9688 | 3,0273 |
| -1,1250 | 3,0313 | -3,4102 |
| -2,1250 | -2,9688 | 6,3086 |
| 3,8750 | -3,9688 | -15,3789 |
| -4,1250 | -3,9688 | 16,3711 |
| -5,1250 | 1,0313 | -5,2852 |
| -3,1250 | 3,0313 | -9,4727 |
| 1,8750 | 4,0313 | 7,5586 |
| -3,1250 | -3,9688 | 12,4023 |
| -3,1250 | 5,0313 | -15,7227 |
| 1,8750 | 2,0313 | 3,8086 |
| -1,1250 | -1,9688 | 2,2148 |
| 2,8750 | -3,9688 | -11,4102 |
| 0,8750 | 0,0313 | 0,0273 |
| -1,1250 | -0,9688 | 1,0898 |
| 2,8750 | 1,0313 | 2,9648 |
| 1,8750 | 3,0313 | 5,6836 |
Součet třetího sloupce, který je nejvíce vpravo, je 33,125, a dělíme ho počtem dat, 32. Výsledek je 1,0352.
Nyní, protože se jedná o 32 dat, mohlo by se jednat o vzorek, takže dělení není mezi n, ale mezi n-1. Výsledek je 1,0685 (33,125/31).
Je třeba poznamenat, že programy jako Excel již mají mezi svými funkcemi tu, která automaticky provádí výpočet kovariance. To platí jak pro populaci, tak pro vzorek. Není nutné provádět výpočet ručně.
Nyní se podívejme na velmi zjednodušený příklad, jak by se počítala kovariance pro seskupená data. V tomto případě je f frekvence, s jakou se opakuje stejný výsledek, jak pro x, tak pro y.
Nejprve se podíváme na neseskupená data:
| x | y | ||
| 3 | 6 | ||
| 4 | 7 | ||
| 3 | 6 | ||
| 3 | 6 | ||
| 4 | 7 | ||
| 5 | 9 | ||
| 4 | 7 | ||
| 5 | 9 | ||
| 2 | 5 | ||
| 6 | 9 |
| x | y |
| 3 | 6 |
| 4 | 7 |
| 3 | 6 |
| 3 | 6 |
| 4 | 7 |
| 5 | 9 |
| 4 | 7 |
| 5 | 9 |
| 2 | 5 |
| 6 | 9 |
Nyní, seskupená:
| x | y | f | |||
| 3 | 6 | 3 | |||
| 4 | 7 | 3 | |||
| 5 | 9 | 2 | |||
| 2 | 5 | 1 | |||
| 6 | 9 | 1 |
| x | y | f |
| 3 | 6 | 3 |
| 4 | 7 | 3 |
| 5 | 9 | 2 |
| 2 | 5 | 1 |
| 6 | 9 | 1 |
| (xi-x) | (yi-y) | (xi-x)*(yi-y)*f | |||
| -0,90 | -1,10 | 2,97 | |||
| 0,10 | -0,10 | -0,03 | |||
| 1,10 | 1,90 | 4,18 | |||
| -1,90 | -2,10 | 3,99 | |||
| 2,10 | 1,90 | 3,99 |
| (xi-x) | (yi-y) | (xi-x)*(yi-y)*f |
| -0,90 | -1,10 | 2,97 |
| 0,10 | -0,10 | -0,03 |
| 1,10 | 1,90 | 4,18 |
| -1,90 | -2,10 | 3,99 |
| 2,10 | 1,90 | 3,99 |
Vyvinuli jsme postup podobný předchozímu příkladu (x a y tučně jsou aritmetické průměry pro každou proměnnou).
Součet třetího sloupce této poslední tabulky je 15,10 a dělíme ho (n-1), předpokládáme, že se jedná o vzorek. Výsledek je 1,6778 (15,10/9).